
An innovative design of knit fabric with auxetic properties
There are mainly two methods to achieve auxetic fabrics. The first one is to use auxetic yarns to fabricate fabrics with normal structures. Miller et al. reported a type of auxetic woven fabric made of auxetic yarns for composite reinforcement and proved that the composite manufactured from two layers of the auxetic fabrics showed an auxetic effect, informs Dr N Gokarneshan and N Varsha.
- Introduction
Poisson’s ratio is defined as the minus value of material lateral strain to longitudinal strain under tension. Although most materials possess a positive Poisson’s ratio theoretically and practically, materials with a negative Poisson’s ratio (NPR) do exist in nature. Materials with a NPR are also known as auxetic materials. They have received increasing attention since the first man-made auxetic foam was reported in 1987.4 Auxetic materials, usually with a special structure, being either macroscopic or microscopic, will expand under unidirectional tension.
Due to this counterintuitive behaviour, properties of auxetic materials, such as shear resistance, indentation resistance, sound absorption and crashworthiness can be enhanced making them ideal materials for many interesting applications, such as personal protection, biomedicine, aerospace and even military use. So far, many structures have been proved to be auxetic and many of them have been found to have similar deformation mechanisms. There are mainly two methods to achieve auxetic fabrics. The first one is to use auxetic yarns to fabricate fabrics with normal structures. Miller et al. reported a type of auxetic woven fabric made of auxetic yarns for composite reinforcement and proved that the composite manufactured from two layers of the auxetic fabrics showed an auxetic effect.
Wright et al. proposed a woven structure fabricated with helical auxetic yarns. Although the Poisson’s ratio of the auxetic yarns used was as low as –1.5, the fabrics made from these auxetic yarns only obtained a Poisson’s ratio of –0.1. Using the same principle, Ng and Hu also fabricated auxetic woven fabrics with different types of auxetic yarns and found that the auxetic effect of the fabrics depended on several parameters, including the yarn arrangements, woven structures and types of helical yarns used. The limitation of using auxetic yarns to produce auxetic fabrics is that their auxetic behaviour could be restrained by the fabric structure. The second method is to directly fabricate auxetic fabrics from non-auxetic yarns by realising special auxetic geometrical structures in fabrics.
Several woven fabrics have been proposed using this method. Knitting has also shown its advantage in fabricating auxetic fabrics using different auxetic geometries. Through flat knitting, Liu et al.28 produced auxetic weft knitted fabrics based on a foldable structure comprised of parallelogram planes. Hu et al. also designed and fabricated three types of auxetic knitted fabrics based on foldable structures, rotating rectangles and reentrant hexagons, respectively. In regard to warp knitting, Ugbolue et al. proposed a type of auxetic structure with the use of thicker soft yarns to form open chain wales and high stiffness yarns as inlaid yarns.
They also suggested a reentrant hexagonal warp knitted structure by using inlaid elastomeric yarns. Alderson et al. developed another type of warp knitted fabric with a double arrow head structure and found that a NPR could be achieved under tension. Wang and Hu developed a special type of auxetic warp knitted spacer fabrics with in-plane auxetic behaviour through the modification of a non-auxetic hexagonal geometry to an auxetic geometry formed with parallelograms by using the thermo-mechanical method. Ma et al. proposed another type of warp knitted fabric with NPR based on a rotational hexagonal structure and further applied it to warp knitted spacer fabrics.
Although a few auxetic warp knitted fabrics have been proposed based on different geometries, the number is still limited and more auxetic warp knitted fabrics can be achieved using novel methods to enlarge their range. This paper reports the design and fabrication of a novel type of planar auxetic warp knitted structure based on a modified reentrant hexagonal geometry by using a conventional high-speed tricot warp knitting machine. It is expected that the newly proposed auxetic warp knitted structure would have great potential for practical applications
- Technical details
The well-known reentrant hexagonal structure, as shown in Fig 1(a), was adopted as the basic geometry to form auxetic warp knitted fabrics. As illustrated in Fig 1(b), there are two types of ribs in a basic unit of the structure, namely the horizontal ribs and the diagonal ribs. When subjected to tension in either the vertical or horizontal directions, the horizontal ribs will remain straight, but the diagonal ribs tend to rotate toward the vertical direction, leading to the lateral extension of the basic unit. As a result, the auxetic effect is achieved. It should be noted that the ribs can be designed to have different lengths to achieve different for obtaining different auxetic effects.
Generally, warp knitted fabrics do not have reentrant geometry. However, warp knitted technology shows its advantage in fabricating net structures that can be transformed into reentrant ones by using special yarn arrangements and lapping movement. In order to design fabrics based on the above-proposed reentrant geometry, a conventional fabric structure with rectangular nets, as shown in Fig 2(a), was used as the basic frame and each rectangular net is comprised of two horizontal ribs, a and b, formed by stiff underlaps, and four vertical ribs, c, d, e and f, formed by stiff wales.
To achieve the reentrant geometry, as shown in Fig 1(a), additional underlaps formed by elastomeric yarns were introduced to connect two adjacent stiff underlaps horizontally. As shown in Fig 2(b), stiff underlaps and elastic underlaps are alternatively distributed along both the wale and course directions. The length and width of both the horizontal and vertical ribs could be designed through changing the number of wales or courses in a repeating unit and the threading method of the warp yarns. As shown in Fig 2(c), elastomeric yarns will shrink after finishing, narrowing the distance between two adjacent vertical ribs, while stiff yarns will support the adjacent vertical ribs to keep a distance between them due to their high stiffness. As a result, the conventional rectangular nets were converted into auxetic reentrant ones. The vertical ribs also become diagonal ribs. Due to the use of elastomeric yarns, the designed auxetic geometry can exhibit much better elastic recovery after the load is released.
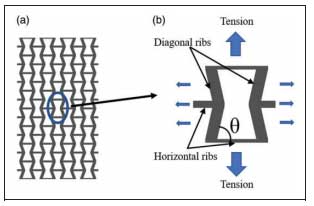
Fig 2: Schematic illustration of the structural design: (a) conventional rectangular nets; (b) introducing elastomeric yarns during the knitting process; (c) conversion of conventional nets into auxetic geometry due to the shrinkage of elastomeric yarns.
Knitting of auxetic warp knitted fabrics The above-designed auxetic geometry can be fabricated with special yarn arrangements and lapping movements using a conventional warp knitting machine. Rigid warp knitted wales and long underlaps are used to form the vertical ribs and horizontal ribs, respectively. It should be noted that the width and length of both the vertical and horizontal ribs can be varied by changing the yarn threading methods and the number of knitting courses in a repeating unit. In this study, to avoid rethreading of yarns, which is time-consuming, the same yarn threading method (two knitting needles and two non-knitting needles in a repeating unit) was used to produce the auxetic fabric samples with different numbers of knitting courses for the vertical ribs (V) and horizontal ribs (H) in a repeating unit to study the influence of the rib size on the auxetic behaviour of fabrics. The loop structures of the three fabrics are schematically shown in Fig 3 and their corresponding chain notations are listed in Table 1.
For easy reference, the values of V and H for each fabric structure are also provided in Table 1. It can be seen that three yarn guide bars (GBs) were used. While the first yarn GB (GB1) was used to knit open chain stitches to stabilise the ground structure for the realisation of the targeted reentrant geometry, the second GB (GB2) and the third GB (GB3) were used to knit tricot stitches for the vertical ribs (cross two-needle space) and the horizontal ribs (cross six-needle space) with symmetrical lapping movements. The use of tricot stitches can enhance the structural stability and stiffness of the vertical ribs. In order to reduce the number of yarn GBs and beams to smoothly fabricate auxetic fabrics on the available warp knitting machine with only four yarn GBs and four beams, the same type of yarns were wound on the same beam and yarns with the same lapping movement were threaded on the same yarn GBs.
As a result, three beams and three yarn GBs were used. The yarns from the first beam were the binding yarns and they were threaded on GB1. The yarns from the second beam were monofilament yarns and they were divided into two groups. Half of them were threaded on GB2 and the other half of them were threaded on GB3. The yarns from the third beam were elastomeric yarns and they were also divided into two groups. Half of them were threaded on GB2 and the other half of them were threaded on GB3. Therefore, the monofilament yarns and elastomeric yarns were alternatively threaded on GB2 and GB3. In this study, the objective was to propose a novel method to fabricate warp knitted fabrics with a NPR. Therefore, only the available common yarns, as shown in Table 2, were used for knitting auxetic fabric samples.
However, it should be noted that, in addition to polyester, other types of monofilaments, elastic yarns and multi-filaments can also be used to replace the yarns used in this research to form stiff underlaps, elastic underlaps and binding stitches, respectively. While the stiff and elastomeric yarns in GB2 and GB3 were used to fabricate the basic reentrant geometry, the binding yarns in GB1 were used to knit chain stitches for preventing yarn slippage under tension in the wale direction. In order to avoid the bending of underlaps due to the shrinking of elastomeric yarns, polyester monofilament with a diameter of 0.1 mm (108 dtex), which was considered to be stiff enough, was selected as the stiff yarn.
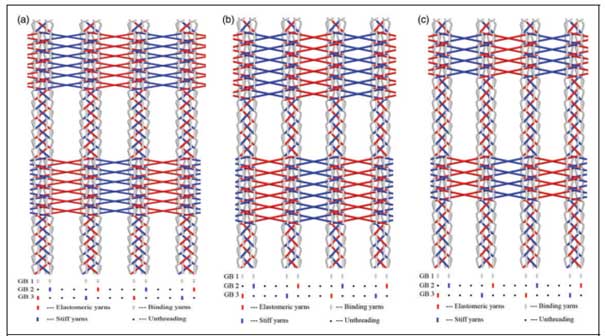
Fig 3: Schematic illustration of fabric structures: (a) Fabric 1; (b) Fabric 2; (c) Fabric 3.
The machine used was a conventional high-speed tricot warp knitting machine. The details of the machine are shown in Table 3. It should be pointed out that a multi-speed electronic letting-off system is necessary for the tension control of warp yarns to help the knitting process go smoothly. For all three fabrics, two-needle space tricot, six-needle space tricot and chain stiches were knitted with let-off values of 1850, 3000 and 1500 mm/rack, respectively. To facilitate the analysis, all the fabrics were fabricated with the same loop course density of 16 courses/cm. Although the speed of the warp knitted machine can reach 1100 rotations per minute (rpm), to fabricate the fabrics safely and smoothly, the speed for fabricating the proposed fabrics was set at 800 rpm.
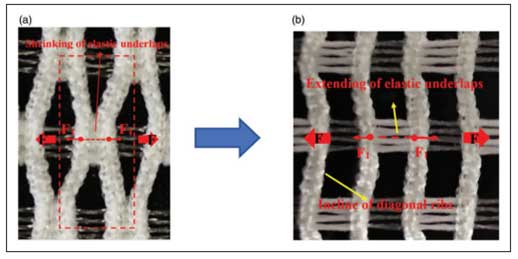
After knitting, all fabrics were subjected to a heat setting process under a temperature of 160oC for 5 minutes to stabilize the reentrant structure. The underlaps formed with elastomeric yarns shrank due to their internal stress, and those formed with stiff yarns remained straight due to their high stiffness. As a result, a reentrant hexagonal geometry was formed in the fabrics. Fig 4 shows the fabrics obtained after the finishing process. It can be seen that the expected reentrant unit cells as designed were achieved and the angles between the horizontal ribs and diagonal ribs are different due to the different diagonal rib lengths in the fabrics.
Tensile test- According to previous studies, the Poisson’s ratio values of fabrics can be obtained through measuring both the lateral and longitudinal dimensional changes of the samples. To facilitate the measurement of dimensional changes, marks should be made at proper positions on the surface of the fabric samples and a better and more effective method was to record the dimensional changes during the test by video. After the test, the photos with marks were extracted from the video for measuring the lateral and longitudinal dimensional changes of the marks using the screen ruler, through which the Poisson’s ratio at a certain tensile strain can be calculated. It should be noted that the lateral dimensional changes can be measured at any position of the samples along the tensile direction. However, the largest lateral dimensional changes are obtained in the middle of the samples due to the constraint of the clamps. In this study, the tensile tests were conducted based on the method adopted by Zulifqar et al.
As the designed reentrant geometry usually has an in-plane auxetic effect in the horizontal and vertical directions, as shown in Fig 1(b), the tensile tests were conducted in the wale direction and the course direction and each test was conducted three times. The size of the testing samples was 200 mm, 50 mm, and all of them were marked with five points. The centre point was set as the datum point and the other four points were set along the tensile direction with a distance of x and the lateral direction with a distance of y to the central point. Values of x and y do not affect the Poisson’s ratio. However, they must be marked parallel to the tensile direction and the lateral direction, respectively. An Instron 5566 machine was used and the tensile tests were conducted at a tensile speed of 50 mm/min with a testing gauge of 150 mm.
During the testing of each sample, a Canon camera was installed in front of the Instron machine to video-record the deformations of the sample. After the tests, the videos were processed in a software named KMPlayer to extract the pictures of fabrics under tension with a time interval of 500 ms. A screen ruler of another software named FastStone Capture was used to precisely measure the changes of pixel numbers between the marks. For each sample, the pixel numbers between the marks in the tensile direction and the lateral direction of the sample picture before testing were measured as the initial pixels v0 and h0, respectively. The pixel numbers between the marks in the tensile direction and the lateral direction of the sample pictures during the tensile process were measured as v and h, respectively. Based on the values obtained, the tensile strain “y and the lateral strain “x can be calculated using Equations (1) and (2), respectively “y ¼ v v0 v0

Fig 4: Photographs of auxetic warp knitted fabrics produced at the unloaded state: (a) Fabric 1; (b) Fabric 2; (c) Fabric 3.
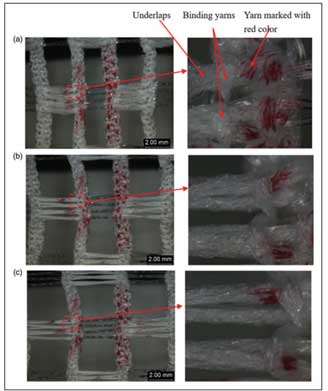
Tensile behaviour Since all three fabrics fabricated were produced based on the same geometry, their auxetic behaviours should be similar. In this regard, one of the fabrics could be selected as a representative fabric to analyze the typical auxetic behaviours of the auxetic warp knitted fabrics in different tensile directions. In this study, Fabric 3 was selected as an example for discussion, and its stress– strain curves are illustrated in Fig 7. It can be seen that the fabric has a much higher extensibility and a lower slope when stretched in the course direction. The main reason for this is that when the fabric is stretched in the course direction, the yarns can be easily transferred from loops in the wales to the underlaps. Fig 8 illustrates how a yarn marked in red colour is transferred from the wale to the underlap when the tensile strain is increasing. The transfer of yarns causes yarn slippage, which results in a lower slope of the stress–strain curve in the course direction. However, when stretched in the wale direction, as it is more difficult for the yarn transfer to take place, the fabric shows a lower extensibility but with a higher slope.
In this case, the yarns in the fabric start to bulk and then break after the tensile strain exceeds 50%, causing the breaking of the fabrics. The lateral strain and Poisson’s ratio as a function of tensile strain when stretched in the course and wale directions are shown in Fig 9(a) and (b), respectively. As the yarns in the fabric start to break, causing the breaking of the fabric when the tensile strain in the wale direction exceeds 50%, the measurement of the Poisson’s ratio in this direction is no longer effective after 50% tensile strain. On the other hand, when the tensile strain exceeds 45% in the course direction, the Poisson’s ratio values change from positive to negative. Therefore, only the testing results within tensile strain of 50% in both. It can be seen that the auxetic effect is achieved in both directions in a large range of tensile strain. However, due to the difference in the lateral strain changes, as shown in Fig 9(a), the auxetic behaviours of the fabric in the two directions are very different.

In addition to having much auxetic behaviour in the wale direction, the variation trends of the auxetic behaviours in both directions are also different. While the auxetic behaviour of the fabric stretched in the course direction decreases with changes of Poisson’s ratio value from negative to positive in a monotone way, the auxetic behaviour of the fabric stretched in the wale direction first increases and then decreases, but keeping a negative value of the Poisson’s ratio until the breaking of the fabric. These different behaviours can be explained by analyzing tensile loading, which leads to the stretch and rotation of ribs Fig 10 shows the deformations of the fabric under tension in the wale direction, in which the dashed box in red represents one basic unit. It can be seen that when subjected to tension in the wale direction, forces F1 created by tensile stress will be exerted along the diagonal ribs.
As F1 is not parallel to the loading direction, two resultant forces F2 with opposite directions in each basic unit will be produced along the horizontal direction. Under the action of F1, the diagonal ribs will be stretched, causing their elongation in length. Under action of F2, the shrunk ribs made of elastomeric yarns will be extended, causing the rotation of the diagonal ribs and expansion of the fabric in the lateral direction. As shown in Fig 10(a), under lower tensile tension, the rigid ribs (underlaps) made with monofilaments can bear pressure of F2, keeping their straight shape. Therefore, a high auxetic behaviour is obtained due to the high extension of the elastic ribs. However, with the increase of tensile strain, the pressure applied by F2 on the rigid ribs increases. High pressure makes the rigid ribs bendresulting in a decrease of the fabric size in the lateral direction but an increase of size in the through-the-thickness direction. In addition, with the increase of tensile strain, the stress exerted on wales by F1 also increases, causing stretching of the diagonal ribs.
As a result, the auxetic behaviour of the fabric decreases. It should be noted that the bending of the stiff underlaps also provides the fabric with an out-of plane auxetic effect due to the increase of the fabric thickness. As this work is focused on the in-plane auxetic behaviour of the fabric, detailed discussion on the auxetic behaviour in the fabric thickness direction will not be conducted here. When stretched in the course direction, both the rigid and elastic ribs (underlaps) will bear the main tensile load. As the loading direction is parallel to the course direction, there is no additional force exerted along the wales. In this case, the extension of elastic underlaps and straightening of stiff underlaps will cause the rotation of the diagonal ribs, resulting in a size increase of the fabric in the lateral direction.
As a result, auxetic behaviour is produced. However, as diagonal ribs made with loops are not very rigid, they can bear tension rather than compression. At lower tensile strain, the rotation of the diagonal ribs can easily increase the size of the fabric in the lateral direction, producing a higher auxetic behaviour. However, with the increase of tensile strain, the diagonal ribs that have been rotated to the vertical direction start to incline and bend due to the flexibility of the ribs and different extensibilities between the rigid and elastic underlaps (horizontal ribs), causing a decrease of fabric size in the lateral direction, as shown in Fig11(b). In addition, as explained before, the transfer of yarns from loops to underlaps under tension in the course direction can also cause a decrease of the auxetic effect.

Effect of knitting parameters
Effect of knitting courses for diagonal ribs
To study the effect of knitting courses for the diagonal ribs (V) on the auxetic behavior of the warp knitted fabrics, Fabrics 1 and 2 were fabricated with the same knitting courses for the horizontal ribs (H) but with different knitting courses for the diagonal ribs (V). The testing results of their Poisson’s ratio as a function of tensile strain when stretched in the wale direction and the course direction, respectively. When stretched in the wale direction, at the initial stage, Fabric 2 shows a slightly higher auxetic effect than that of Fabric 1. However, with the increase of tensile strain, the auxetic effect of Fabric 1 becomes better than that of Fabric. When stretched in the course direction, as shown in Fig 12(b), the two fabrics show almost the same auxetic effect, and the lateral strain of Fabric 2 decreases much faster than that of Fabric 1 after the Poisson’s ratio becomes positive.
The above differences in auxetic behaviour of the two fabrics can also be explained by analyzing the tensile loading applied in different directions. As shown in Fig 1(b), is the angle formed between the adjacent horizontal ribs and diagonal ribs. As H is constant, the horizontal ribs (underlaps) in the two fabric structures are the same. As shown in Fig 4, Fabric 1 has a larger than Fabric 2 according to the measurement, due to longer diagonal ribs. Due to the smaller value of in Fabric 2, when stretched in the wale direction, the angle between F1 in Fabric 2 is smaller than that of Fabric 1, which leads to a larger F2, as shown in Fig 10. Under the action of F2, the shrunk ribs made of elastomeric yarns will be extended and a larger value of F2, causes greater expanding of the elastic ribs.
Since at the initial stage the lateral strain change mainly comes from the expanding of elastic underlaps or the rotation of the diagonal ribs, a better auxetic effect is obtained for Fabric 2. However, with the increase of the strain, the lateral strain change mainly comes from the bending of stiff underlaps. As F2 in Fabric 2 is higher than that in Fabric 1, the bending of the stiff underlaps of Fabric 2 is higher than that of Fabric 1, which results in a less lateral expanding of Fabric 2. As a result, the auxetic effect of Fabric 1 becomes better than that of Fabric 2. When stretched in the course direction, at the initial stage, the lateral strain change mainly comes from the rotation of the diagonal ribs. As mentioned above, the diagonal ribs are comprised of flexible loops, which are very easily deformed. Although the length of the diagonal ribs is different in the two fabrics, the flexibility of the diagonal ribs in the two fabrics is the same. Therefore, the lateral expansion effects of the two fabrics due to the rotation of diagonal ribs are not very different, which result in almost the same auxetic behaviour. With the increase of the strain, the transfer of yarns from loops to underlaps becomes the main factor.
The shortening of diagonal ribs due to yarn transfer causes the change of the Poisson’s ratio from negative to positive. Due to the smaller value of V of Fabric 2, the shortening effect of diagonal ribs in Fabric 2 becomes more important than in Fabric 1, which results in the higher positive Poisson’s ratio of Fabric 2. Effect of knitting courses for horizontal ribs (H) To study the effect of the knitting courses for horizontal ribs on the auxetic effect, Fabrics 1 and 3 were fabricated with the same knitting courses for diagonal ribs (V) but with different knitting courses for horizontal ribs (H). The test results of the two fabrics in the wale and course directions. It can be seen that the effect of H is quite evident in the two tensile directions. When stretched in the wale direction, the auxetic effect of Fabric 3 is higher than that of Fabric 1 when the tensile strain is lower than 30%.
However, with the increase of tensile strain, the auxetic behaviour of the two fabrics becomes almost the same. When stretched in the course direction, there is no great difference of auxetic effect in the two fabrics at the initial stage. However, with the increase of tensile strain, the auxetic effect of Fabric 1 decreases much faster than that of Fabric 3. The different auxetic behaviours of the two fabrics when stretched in the wale direction can be explained by the different ability of diagonal rib orientation. When stretched in the wale direction, the lateral strain change mainly comes from the expanding of elastic underlaps at the initial stage. As the value of H is smaller in Fabric 3, the number of elastic underlaps of Fabric 3 in one basic unit is less than that of Fabric 1, which means less stress is needed for the same expanding of the underlaps. Therefore, the rotation of diagonal ribs in Fabric 3 is much easier than that in Fabric 1.
As a result, the degree of orientation for diagonal ribs in Fabric 3 for a given strain is larger than that in Fabric 1, leading to a larger expanding of elastic underlaps, producing a larger auxetic effect. With the increase of tensile strain, the lateral strain change mainly comes from the bending of stiff underlaps. In this stage, due to the less stiff underlaps of Fabric 3 in one basic unit, the stiff underlaps are much easier to bend to the outside of plane. As a result, the lateral strain of Fabric 3 decreases much faster than that of Fabric 1. However, with the further increase of tensile strain, the orientation degree of the diagonal ribs in the two fabrics tends to be almost the same. Therefore, the two fabrics demonstrate almost the same auxetic behaviour after the tensile strain exceeds 30%. When stretched in the course direction, the difference of auxetic behaviour may come from the transfer of yarns from loops to underlaps. As there are more underlaps within a unit cell in Fabric 1 than that of Fabric 3, more loops in Fabric 1 will shrink for a given tensile strain, leading to higher shrinkage in the lateral direction. As a result, the auxetic behaviour of Fabric 1 decreases much faster than that of Fabric 3, with a faster change of Poisson’s ratio value from negative to positive.
Conclusions
A novel type of auxetic warp knitted structure was first designed based on the modification of a non-auxetic geometry to a re-entrant auxetic structure. Various auxetic fabrics were then fabricated using a conventional warp knitting machine with different knitting parameters. The fabric samples obtained were finally tested to assess their auxetic behaviour. Based on the test results, the following conclusions can be obtained.
- Auxetic warp knitted structures can be achieved using elastomeric yarns and stiff yarns in a special arrangement on a warp knitting machine with more than three yarn GBs. This technique not only expands the method of knitting auxetic fabrics using warp knitting technology, but also make it possible to manufacture auxetic fabrics using conventional machines with conventional yarns.
- The use of binding yarn is necessary to fabricate auxetic warp knitted fabrics with a stable structure. Binding yarns should be used in the front bar to get the binding effect.
- The auxetic knitted fabrics have obvious auxetic behaviour in both the wale and course directions. When stretched in the wale direction, the fabrics can retain the auxetic effect until breaking. However, when stretched in the course direction, the Poisson’s ratio can change from negative to positive when the tensile strain exceeds some limited values.
- The knitting courses for the diagonal ribs and horizontal ribs (underlaps) in a unit cell have an obvious effect on the auxetic behaviour. As this is only a primary study, some limitations still exist. For example, the geometrical model used to study the relationships between the parameters and the Poisson’s ratio of the structures has not been set up and the auxetic behaviours in off-axis directions are not clear. Besides, the stability of the auxetic effect has not been tested. Therefore, future work will be focused on the establishment of geometrical models, the testing of the fabrics in off-axis directions and the study of auxetic stability. Finally, as the objective of this paper is to propose a novel method to fabricate auxetic warp knitted fabrics, only the available polyester yarns were used in this study. A comparison of using different types of yarns to realize the same warp knitted structure can also be another future research direction.
References
1. Ma P, et al. Review on the knitted structures with auxetic effect. J Text Inst 2017; 108: 947–961.
2. Evans KE and Alderson A. Auxetic materials: functional materials and structures from lateral thinking! Adv Mater 2000; 12: 617–628.
3. Lim T-C. Auxetic materials and structures. Singapore: Springer, 2015.
4. Lakes R. Foam structures with a negative Poisson’s ratio. Science 1987; 235: 1038–1041.
5. Hu H and Zulifqar A. Auxetic textile materials-a review. J Text Eng Fashion Technol 2016; 1: 00002.
6. Grima JN, et al. On the auxetic properties of rotating rhombi and parallelograms: a preliminary
investigation. Phys Status Solidi b 2008; 245: 521–529.
7. Liu Y and Hu H. A review on auxetic structures and polymeric materials. Sci Res Ess 2010; 5: 1052–1063.
8. Scarpa F and Tomlin P. On the transverse shear modulus of negative Poisson’s ratio honeycomb structures. Fatigue Fract Eng Mater Struct 2000; 23: 717–720.
9. Lakes R and Elms K. Indentability of conventional and negative Poisson’s ratio foams. J Compos Mater 1993; 27: 1193–1202.
10. Alderson K, et al. An experimental study of ultrasonic attenuation in microporous polyethylene. Appl Acoust 1997; 50: 23–33.
About the author: Dr N Gokarneshan is presently working as professor at the department of Fashion Design at Hindustan Institute of Technology and Science, Chennai and is research supervisor for 5 scholars. He has a stint of over 25 years in education and about 10 years in industry. He worked in premier institutions like PSG College of Technology, Kumaraguru College of Technology, Bannariamman Institute of Technology, etc.



