Achieving yarn quality using control charts

Yarn testing and quality control charts are significant things in the yarn industry that we can give the quality assurance of yarn products

Due to expanding global markets, representing competition between companies to provide high-quality products and goods follows consumer satisfaction. Better control gives the philosophy and riding force for designing first-class to please the customers by specialising in the satisfactory value of an organisation’s services and products.

1. Introduction

The fundamental goal of quality control is to ensure that the goods, services, or strategies provided meet precise requirements and are reliable, high-quality, and less costly and bodily sound quality control in textiles industries is concerned with being certain a product meets performance standards and customer expectations.

 A control chart is applied because the most critical device of statistical technique manipulates this is regularly hired to determine whether or not a technique in statistical control. The control chart refers to a graphic show of a satisfactory feature that has been r determined from samples as opposed to the pattern quantity or time. Variable manage charts are used to display non-stop traits of the products, at the same time characteristic control charts are implemented to reveal the satisfactory traits, which are not feasible to specify on a numerical scale.

 In yarn production, attempting out targeted on three areas: stop-product trying out of traits such as linear density, twist, strength and elongation, brief-time period evenness, and count variant; inspection of defects which includes thick and skinny locations, and repeating faults like mechanical errors or drafting waves; and frequency checks for preventing breaks at some stage in spinning. Yarn count, energy, elongation, twist, and hairiness are actually all frequently analysed.

This research study is an attempt to aid the textile producers and to increase their competitive position in the globe by focusing on ways of reducing quality costs in their respective unit operations especially in a competitive market or in a recession environment. The quality control tool presented in this research study is not without limitations, but also to address and improve the current quality issues and challenges faced by the textile. Excellent improvement of final products increases producers’ competitiveness in addition to lowering charges. Therefore, automatic methods for monitoring satisfactory characteristics based on vision are nevertheless in development. Prepare charts for a controlling count of given cotton yarn, used the result on a graph chart, and discuss the results. This paper is done for determining the defect of yarn and producing the same quality from all machines. This paper provides an analytical study of statistical process control of the yarn count of variable control charts commonly used.

Ahmed et al. first time apply the control charts in the textile spinning industry to monitor the yarn quality characteristics without considering any condition for selecting suitable control charts. Yeh et al. proposed a new control chart model to effectively monitor small changes in the variability of multivariate normal processes. For designing the new control chart, they first studied the evolution of multivariate control charts to monitor and analyse the variability of the multivariate normal process. Kan and Lau studied the effect of sampling methods (regular and random sampling) on yarn satisfaction by using the use of T-check, and R manage charts and decided that random sampling outcomes are more dependable than regular sampling. Faraz and Moghadam as an alternative to the traditional control charts for uncertain datasets. Felili and Fekraty constructed the control charts on the concept of danger and fuzzy idea to show the yarn fine. They’ve got to discover that fuzzy concept performs higher than opportunity idea for monitoring product nice. Feng and Kapur discussed in element why Shewhart control charts are not powerful at all times particularly in cloth manufacturing. Maros et al. applied control charts on chenille yarns defect kinds to decide the versions.

The records located to be auto correlated, consequently they carried out AR and EWMA kinds manipulate charts for tracking and detecting defects in yarn sorts. Reynolds Jr. Et al suggest that big and transient shifts might be efficiently and efficiently detected simplest via the traditional Shewhart manipulate charts and hence, they have got sizable packages in manufacturing even today. Amjad et al. proposed fuzzy manage chart is indistinct, obscure, uncertain, and incomplete facts and based on α-level fuzzy midrange for α – reduce technique. Aslam developed the neuromorphic logic-based control charts which are termed neuromorphic SPC. The monitoring production processes through the analysis of variance based on the neuromorphic statistics. Samaranayake introduced neuromorphic statistics using the idea of neutropenic logic. The latter branch of statistics is termed neuromorphic statistics, which deals with datasets of uncertain nature or come from some complex system.

As the available literature shows that no study has been conducted to monitor the yarn count quality appropriately. So, here our purpose is to apply the control charts with appropriate conditions to monitor yarn quality. The main logic of this application is to monitored yarn count quality for reducing the yarn waste and improving the yarn quality to satisfy the knitter and weaver customers.

2. Research methods and materials

The control chart is a graph technique used to study how a process changes over time and to routinely monitor quality, depending on the number of process characteristics to be monitored. The data collection is plotted in time order where the manage chart constantly has a central line for the average, an upper line for the higher manage limit, and a decreasing line for the decrease manage limit. The control chart lines are determined from ancient information. The best control chart has been developed over the latest periods, where many techniques have been addressed depending on the situation.

In this paper, a framework control chart method has been applied where involves variable control charts to detect optimal limits for improving the quality of the yarn products. the proposed control chart methodology as shown in (Figure 1) is focused on applying traditional control charts. The framework of the methodology includes problem definition, data collection, selection of the control chart type, establishing the control chart limits, analysis of the results, and decision making will be explained in detail in the next subsequent sections.

Figure 1: The frame work of control

2.1 Control chart types

The control chart is considered a graphical illustration of the gathered records. Additionally, control chart called Shewhart charts, process conduct charts in statistical approach manage used to decide if a production or business technique is in statistical control. A control chart shows product or process is in or out of control. It determines procedures variability and detects uncommon versions taking region in a manner. It provides facts about the choice of method and placing of tolerance limits. The control chart as shown in Figure (2) has a Centreline (CL) and Upper_Control_Limit (UCL) and lower_Control_Limit (LCL). A CL outlines the rate value of the performance characteristic corresponding to in-control status, whereas the UCL and LCL refer to the control boundary anywhere all the sample values drawn between them that mean the process in-control.

Figure 2: Control limits of typical control chart

I. 𝑿̅- R control charts

Several performance characteristics can be represented as expression numerical values. One of the perfect techniques of identifying the process state in control or not is examining the process mean and variability. 𝑋̅-Chart is applied for controlling the mean, while R-chart is applied for controlling the changeability of variables.
Construct the control limits of the 𝑋̅-R chart using the following models:
⦁ X̅- Chart control model …………… (1)

Center Line (CL) = 𝑋̿
Lower Control Limit (LCL) = 𝑋̿– 𝐴2𝑅̅
Upper Control Limit (UCL) =𝑋̿+ 𝐴2𝑅̅)

⦁ R – Chart control model …………… (2)
Center Line (CL) = 𝑅̅
Lower Control Limit (LCL) = 𝐷3𝑅̅
Upper Control Limit (UCL) = 𝐷4𝑅̅

II. 𝐗̅ – S Control charts

Despite the 𝑋̅-R chart is broadly applied, It’s sometimes preferable to estimate the process standard deviation directly rather than indirectly using the range R. This drive for 𝐗̅-S control chart, where S-chart is represented standard deviation.
Construct the control limits of the 𝑿̅-S chart using the following models [3]:
⦁ X̅ Chart control Model ……………. (3)

Center Line (CL) = 𝑋̿
Lower Control Limit (LCL) = 𝑋̿ – 𝐴3𝑆̅
Upper Control Limit (UCL) =𝑋̿ + 𝐴3𝑆̅
⦁ S Chart control Model ……………. (4)

Center Line (CL) = 𝑆̅
Lower Control Limit (LCL) = 𝐵3𝑆̅
Upper Control Limit (UCL) = 𝐵4𝑆̅
Where: X.1 , X.2 , . . . , X.n are variables of sample size n,
The average sample size n:
𝐗̅ = X.1+ X.2+⋯+X.nn ….………..… (5)
X̅. 1 , X̅. 2 , . . . , X̅. m represents the average of each sample,
The grand average:
X.̿ = X̅.1+ X̅ .2 +⋯+X̅ .m m …………… (6)
The range of the sample size n:
R = 𝑋.𝑚𝑎𝑥 – 𝑋.𝑚𝑖𝑛 …………… (7)
Let 𝑅.1 , 𝑅.2 , . . ., 𝑅.𝑚 be the ranges of m samples,
The average of the range:
𝑹̅ = 𝑅.1+ 𝑅.2+⋯+𝑅.𝑚𝑚 …………… (8)
The sample standard deviation:
S =√Σ(𝑋𝑖 −𝑿̅)²𝑛𝑖=1𝑛−1 ….………… (9)

The average of standard deviations:
S̅ = 1mΣSimi=1 …..………… (10)
A2, D3, D4 , A3 , B3 , B4 are constants depending on the sample (observation) size and are tabulated for various sample sizes in tables.
So, 𝑋̅-R and 𝑋̅-S charts are selected to show the process changes and are affected by changes in process variability to secure information in establishing or modifying processes, inspection procedures. These charts when used together form a powerful instrument for diagnosing quality problems.

2.2 Yarn quality monitoring

Yarn is described as “a continuous, twisted strand of cotton successfully fibres which has received its final attenuation and which has been twisted sufficiently, given the energy critical to make possible its use in specific production operations”.

So, the technique of converting fibre into yarn is called yarn production spinning manner and consists of the following departments as illustrated in (Figure 3).The maximum crucial machine for creating excessive outstanding yarn in a cloth is Ring Spinning. Spinning is the set of the technique used in the manufacturing of yarns. The fundamental manufacturing system of spinning is composed of blending, carding, combing, drafting, twisting, and winding.

Quality control plays a vital role in yarn quality especially testing yarn which consists of the count, twist, evenness testing, yarn strength, etc. The quality assessment of yarn explains the properties and characteristics of the yarn quality. Therefore, it is very important to examine and inspect the physical and mechanical properties of the yarn. To examine tests using special instruments should be calibrated and set according to the quality yarn standards.

Figure 3: Yarn manufacturing spinning process

⦁ Yarn spinning machine: At the yarn spinning phase, a raw material used is cotton fibers should be prepared. Cotton fibres arrive from compressed bales in the mill stage. The raw material of cotton fibers must be handled more for the forming of yarn, starting from blow room to ring spinning machine. Ring-spun yarn production includes roving hung the creel above the drafting zone of the ring-spinning machine.
⦁ Yarn testing device: The yarn test method is a significant task in the textile industry and yarn production to examine the characteristics of yarn quality according to international yarn standards. the raw material of yarn is considered very important for the production of high yarn quality. Testing of yarn represents a bridge to help the researchers to prove and to challenge their results. The yarn properties that should be tested include; yarn count, yarn elongation, and yarn strength.

Count yarn tester

The yarn purity often expresses the linear density or count of the yarn lea. A yarn lea five samples are produced in this manner for 120 yards to determine the weight of yarn lea on the weighing device, after that testing the yarn count. So, the yarn count is calculated by the following mathematical model:
Co = Le * 8.33 / Weg …..………… (11)
1_gram = 15.43 grains …..………… (12)
Co = Le / Wep …..………… (13)
Where: Co = The Count yarn
Le = Length in yards
Weg= Weight in grains
Wep= Weight in pounds

Yarn strength and elongation tester

The strength and elongation represent very important factors of yarn performance when used in a real application. yarn strength testing is based on the single yarn strength testing method. The strength and elongation parameters are examined by Uster_Tensorapid4. The digital strength testing setting the Uster_Tensorapid_4 to determine the breaking force of the to correspond with elongation of the technical yarn type. Firstly, yarn strength was tested by Uster_Tensorapid_4. The basic data was measured for evaluation and these values have been transmitted to the control unit to output as final reports.

3. Control charts implementation

As we know the quality control system in most of Iraq’s industries is poor and most of them do not want to share data for confidentiality issues. Therefore, collecting practical raw data required is a great challenge. In this research, a textile factory in the Wasit company for the yarn industry is selected as a case study to apply the research method. The Wasit Company is one of the important companies in the textile industries in Iraq, which is affiliated with the ministry of industry and minerals. In the textile factory, the spinning stage includes several processes are cleaning, opening, carding, drawing, roving, and spinning. Cotton yarns were manufactured by conventional spinning frames from the cotton fibre.

As mention above, yarn data collection is a critical issue to solve problems and to accomplish the objectives. so, the researchers have been able to gather yarn data with full assurance and privacy. The yarn data have been obtained from producing 100 per cent cotton yarn in Iraq. The factory doing the measurements orderly via production to guarantee the results achieved. The count 1/27Ne of cotton on one machine used to produce yarn. The laboratory conditions in the factory are corresponding to the standard atmospheric to get yarn characteristics measurements values. The random sampling method was adopted for collecting data concerning yarn counts to obtain reliable final results. The sample size is 30 readings for 1/2 7 Ne count while the subgroup size is 5 readings. Table (1) shows yarn counts value which has been recorded during thirty days which have been taken to implement of variable control chart. The data shows three characteristics of yarn quality among different threads that production in yarn factory.

According to the data collected concerned with the yarn count obtained from the case study, 𝑋 ̅-R and 𝑋 ̅-S control charts for variables have been applied and implemented to monitor the yarn quality variations as shown in Figure (4). The 𝑋 ̅-R control chart is applied for detection of the changeability in the average of yarn quality and to examine the variation in yarn quality when subgroup size is less than ten and yarn quality follows a normal distribution. While the 𝑋 ̅-S control chart is applied when the subgroup size is greater than or equal to ten. The control limits for both control charts are used to test and monitor, whether yarn count quality in the Ring frame stage was in control or not. The control charts are monitoring process variables by following the R and SD at each subgroup. The control limits for the subgroup means are A2 and A3 were statistical determining constant for R and SD respectively.

The control limits concerned with the subgroup R and the subgroup SD are of the form B3 and B4 respectively where B3 and B4 are also statistical determining constants. For the all control charts used in this work, the UCL and LCLcontrol limits, as well as the CL, are then calculated. MINITAB software is used to enter the obtained yarn data to draw the relation between the response variable and affecting factors. In each case, one response variable listed above of yarn properties are defined as effecting factors in the software.

a1: 𝑋 ̅-R Chart of cN/tex a2: 𝑋 ̅-S Chart of cN/tex
b1: 𝑿 ̅-R Chart of E% b2: 𝑿 ̅-S Chart of E% c1: 𝑿 ̅-R Chart of CVm % c2: 𝑿 ̅-S Chart of CVm %

4. Results discussion

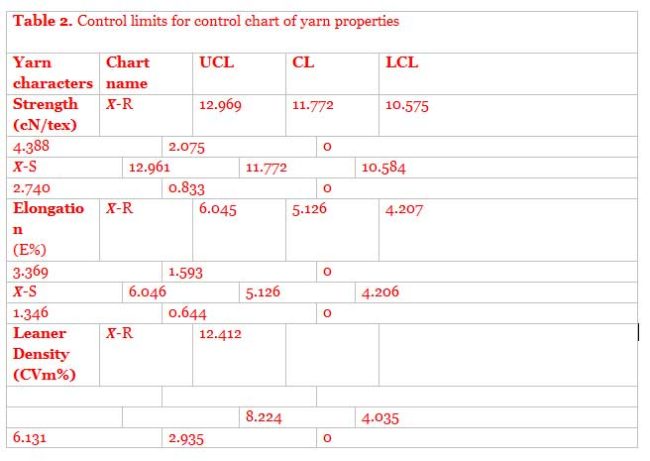
In this study quality control in Iraq’s Wasit company for textile industries has been done. In this stage, the objective was to determine the proper R and SD of the parameters for the spinning to control yarn quality. Results analysis in the tables (2) shows the summary results of the yarn control charts covered in the study. The UCL and LCL values of control charts are shown in the table below of yarn charecteristics that refer to the process control is under control.
The 𝑋̅-charts show the process statistically is not in control, some point values are out of the UCL. R-charts are not in control points also there are some points out of the CL. So, the process is not in a state of statistical control. So, we can see the 𝑋̅-R charts above are not in statistical control. This means that the process is inconsistent and not predictable.

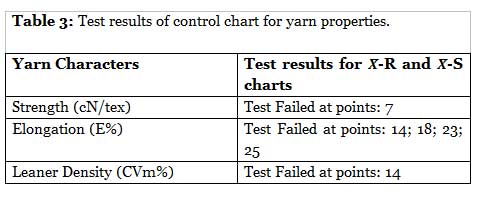
The 𝑋̅-S charts shown above are statistically controlled. This indicates that the procedure is repeatable and consistent. There are only a few frequent reasons for variation. It indicates that subgroup variation is constant from one subgroup to the next. Between these standard deviations, there is no statistical difference. From the above graph, we can see that all of the data are between control limits UCL and LCL as illustrated in Table (3), and other data are not properly distributed. So, the process is under control. From the above chart, we can see that the process is in control on an aggregate basis, although certain points indicate slight instability in the process. Nevertheless, the process is fairly random around the mean. It is, thus, conclude the trial control limits can be adopted for future periods.

5. Conclusion

These conclusions are taken from the above study as follows:
A statistical control charts method was proposed that allows the quality control department to examine the process performance over time. Control charts are a very effective way to judge the process stability. The process is statistically controlled, the control limits are extended into the future, where process performance monitoring utilising these control limits. The control charts reveal that there are particular reasons for variation, to discover and eliminate the reason for variation from the process particularly. Any spinning mill can examine the process stability by using the control charts as used in this study. Recalculate statistical control limits based on that data to use those limits in the future. Yarn testing and quality control charts are significant things in the yarn industry that we can give the quality assurance of yarn products. While it contributes to ensuring performance, the testing and quality control must be carried out extremely carefully and requires competent personnel. Our research mainly consisted of monitoring yarn quality based on control charts from yarn properties by the analyst of data charts. we recommended in future work using advanced methods to monitor yarn quality such as regression, fuzzy logic, and artificial neural networks .. etc. to obtain better results.

7. References

[1] M.F. Zarandi, A. Alaeddini, and I. Turksen 2008 Information Sciences, 178 1152–1170
[2] A. Faraz, R.B. Kazemzadeh, M.B. Moghadam and A. Bazdar 2010 Quality Quantity, 44 905–914
[3] D. Wang and O. Hryniewicz 2015 International Journal of Applied Mathematics-Computer Science, 25 389–401.
[4] M.Z. Khan, M.F. Khan, M. Aslam, S.T.A. Niaki and A.R. Mughal 2018 Information Sciences, 9 312.
[5] F. Smarandache, 2010 Multi space multiseriate. Neutron sophistries disciplinarity, 4 396
[6] Ahmed, M.S., I. Javed, M. Ahmed, H.M. Naeem, & M. Sarwar 1992 Pakistan Journal of Agricultural Sciences 29(1): 25-30.
[7] Yeh AB, Huwang LC, Wu YF 2004 IIE Transactions, 36: 865–879.
[8] Kan, C.W. & M.P. Lau. 2007 Research Journal of Textile and Apparel 11(4): 71-79 (2007).
[9] A. Faraz and M.B. Moghadam 2007 Quality Quantity, 41 375–385
[10] Feili, H.R. & P. Fekraty 2010 The Journal of Mathematics and Computer Science 1(4): 258-272 (2010).
[11] Feng, Q and Kapur, K.C 2009 Operations Research Applications, CRC Press.
[12] Maros, T., B. Viladimir, & T.M. Caner 2011 Textile Research Journal 81(13): 1344-1353 (2011).
[13] Reynolds, M.R., Jr. & Cho, Gyo-Young 2011 Sequential Analysis, Jan- Mar 2011, Vol. 30 Issue 1, p1-40.
[14] Amjad, B. Abdulghafour, Hussien, S., Ghulam, Jamal Z., & Rashed, M. K. 2017 International Journal, 5(1), 8-21.
[15] M. Aslam, A new sampling plan using neuromorphic process loss consideration. Symmetry, 10 (2018) 132.
[16] F. Smarandache, 2014 Romania-Educational Publisher, Columbus, Ohio, USA, Craiova (2014), p. 123 system. IEEE Access, 7 (2019) 15367–15374.

17. Amjad B. Abdulghafour et al 2021 J. Phys.: Conf. Ser. 1973 012158